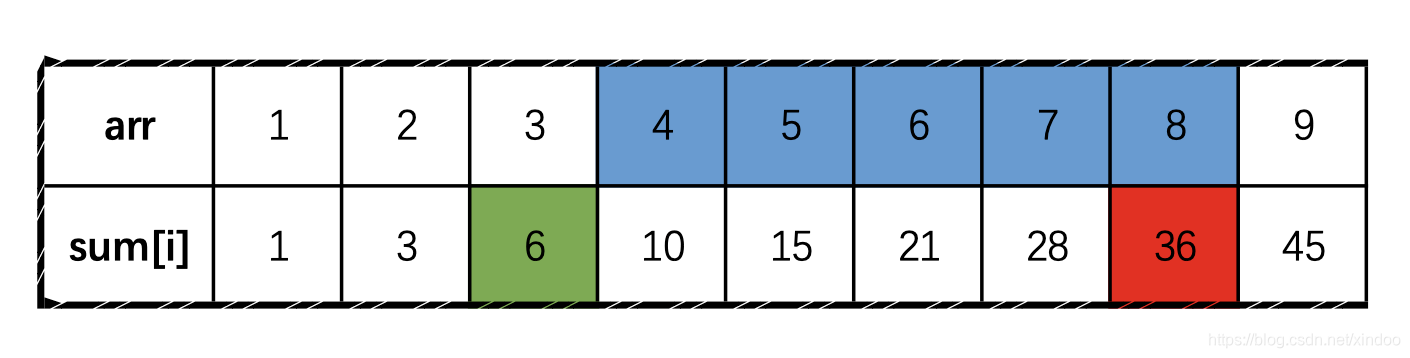
在一个有序数组中找中位数,但需要支持再数组中添加新的元素。本来是有序里的,可以很轻易就查到中位数,但如果添加新数字后,不一定有序。如果先对数组排序,那代价就比较大了,每次排序时间复杂度O(n*log(n)),看discuss发现了一种很巧妙的解法,可以把添加数据的时间复杂度降低到O(log(n)) ,查询中位数O(1)。
这里我们需要用到优先队列,java里有现场的优先队列。准备两个优先队列,large里存比中位数大的数,small里存比中位数小的数。加入现在有n个数,large里存最大的n/2个数,很容易理解。但small里怎么存最小的n/2个数? 这里有个很巧妙的地方,把数组里数取负存到small里,small优先队列里其实存的是数组中取负后最大的n/2个数,不就是原数组中最小的n/2个数吗?需要特别考虑到n位奇数时,large里存了n/2+1个数,small里存了n/2个数(其实多余的一个也存small里)。算中位数的时候,如果n为奇数,直接从large里去第一优先级的就好了,如果n是偶数,从large和small里各取一个求平均,注意small里取出的数要取负变换之后才能用。
代码如下,
import java.util.PriorityQueue;
import java.util.Queue;
class MedianFinder {
private Queue<Long> small = new PriorityQueue();
private Queue<Long> large = new PriorityQueue();
/** initialize your data structure here. */
public MedianFinder() {
}
public void addNum(int num) {
large.add((long) num);
small.add(-large.poll());
if (large.size() < small.size())
large.add(-small.poll());
}
public double findMedian() {
return large.size() > small.size() ? large.peek() : (large.peek() - small.peek()) / 2.0;
}
}