Write a program to find the nth super ugly number.
Super ugly numbers are positive numbers whose all prime factors are in the given prime list primes of size k. For example, [1, 2, 4, 7, 8, 13, 14, 16, 19, 26, 28, 32] is the sequence of the first 12 super ugly numbers given primes = [2, 7, 13, 19] of size 4.
原题链接:Super Ugly Number
题目翻译成中文是『超级丑数』,啥叫丑数?丑数就是素因子只有2,3,5的数,7 14 21不是丑数,因为他们都有7这个素数因子。 这里的超级丑数只是对丑数的一个扩展,超级丑数的素因子不再仅限于2 3 5,而是由题目给定一个素数数组。与朴素丑数算法相比,只是将素因子变了而已,解法还是和朴素丑数一致的。
之前我说过,凡是任何编程问题都有暴力的解法,此题也一样,大不了对每个数求其所有素因子,然后再判断改素因子是否在给定的数组中,n个数求素因子的算法时间复杂度就是O(n^2)了,何况第n个超级丑数会远大于n,所以凡事不要老想着暴力解决,最好动动脑子。
我们先来看看丑数数组存在的一个性质,假设我们已经有了一个丑数数组uglys[n],该数组从小到大保存了所有的丑数。那么绝对存在一个x,使得uglys[x]乘以2或3或5等于uglys[i],且x< i。 通俗易懂的解释就是,第i个丑数就是前面i-1个丑数中的某个丑数乘以2 3或5得到的。这条性质成立就是因为丑数的定义是他除了2 3 5没有其他素因子,而非素因子肯定都可以转化为几个素数相乘。 推而广之,这条性质在超级丑数中也成立,理解了这条性质代码也就很好写了。 我们可以通过已知的丑数乘以2 3或5来获得下一个未知的丑数,但未了保证有序,我们每次只取最小的一个。代码如下。
public class Solution {
public int nthSuperUglyNumber(int n, int[] primes) {
int k = primes.length;
int[] uglys = new int[n];
int[] p = new int[k];
uglys[0] = 1;
for (int i = 1; i < n; i++) {
for (int j = 0; j < k; j++) {
while (primes[j] * uglys[p[j]] <= uglys[i-i]) {
p[j]++;
}
}
uglys[i] = Integer.MAX_VALUE;
for (int j = 0; j < k; j++) {
if (primes[j] * uglys[p[j]] > uglys[i - 1]) {
uglys[i] = Math.min(primes[j] * uglys[p[j]], uglys[i]);
}
}
}
return uglys[n-1];
}
public static void main(String[] args) {
Solution s = new Solution();
int[] primes = {2, 7, 13, 19, 23, 19, 31, 37, 41, 47, 51, 53, 57, 59, 61, 67, 69, 71, 73};
System.out.println(s.nthSuperUglyNumber(1000000, primes));
}
}
可能大家对p数组在这里的意义会有点不理解,p只是一个优化而已。uglys[i]是i前面某个数乘以某个素数,primes素组是免不了要遍历的,但uglys可以不用遍历啊,因为我们再求uglys[i-1]的时候已经验证了某个丑数即便是乘以任意一个给定的素数也不会大于uglys[i-1]的,这里我们需要维护一个性质,任意一个j使得p[j]*primes[j] > uglys[i-1]。
多数一句,看下数据量,n最大是1000000,k最大是100,所以整个代码最内层循环最大应该是100m,这样算法能在几十毫秒解掉此题,看来leetcode的数据比较水。


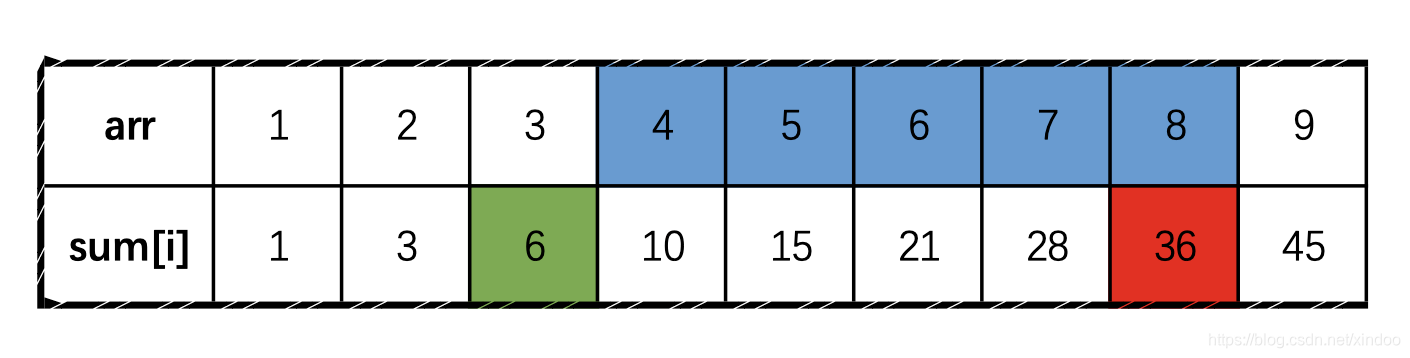


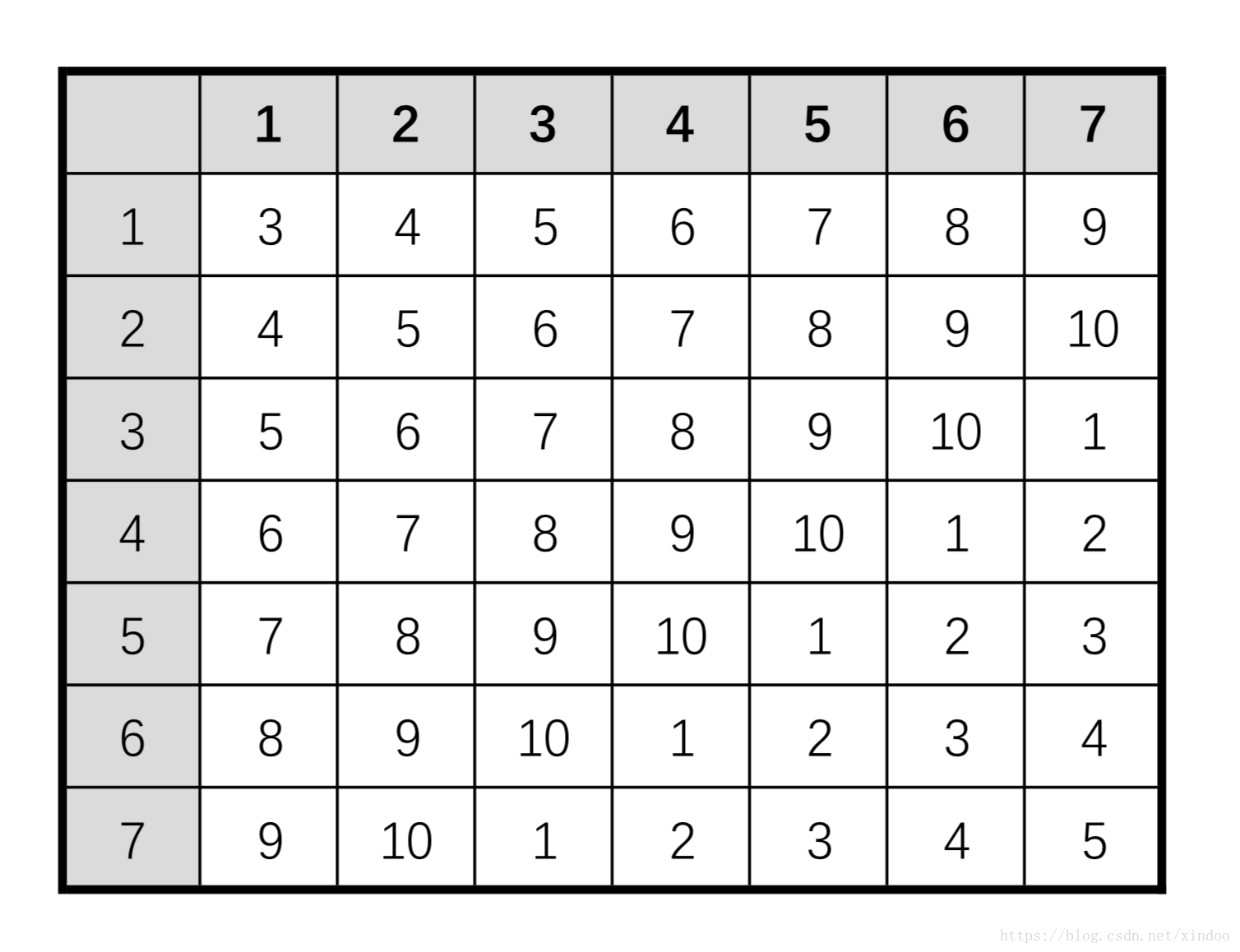

神奇, 虽然看不懂
其实并不复杂的,多思考下就理解了。