斐波那契数列,其最开始的几项是0、1、1、2、3、5、8、13、21、34…… ,后面的每一项是前两项之和,事实上,斐波那契在数学上有自己的严格递归定义。
f0 = 0
f1 = 1
f(n) = f(n-1) + f(n-2)
斐波那契数列其实有很多有趣的性质,比如你拿斐波那契里每项数为半径绘制1/4圆弧,你就会得到著名的黄金螺旋线。
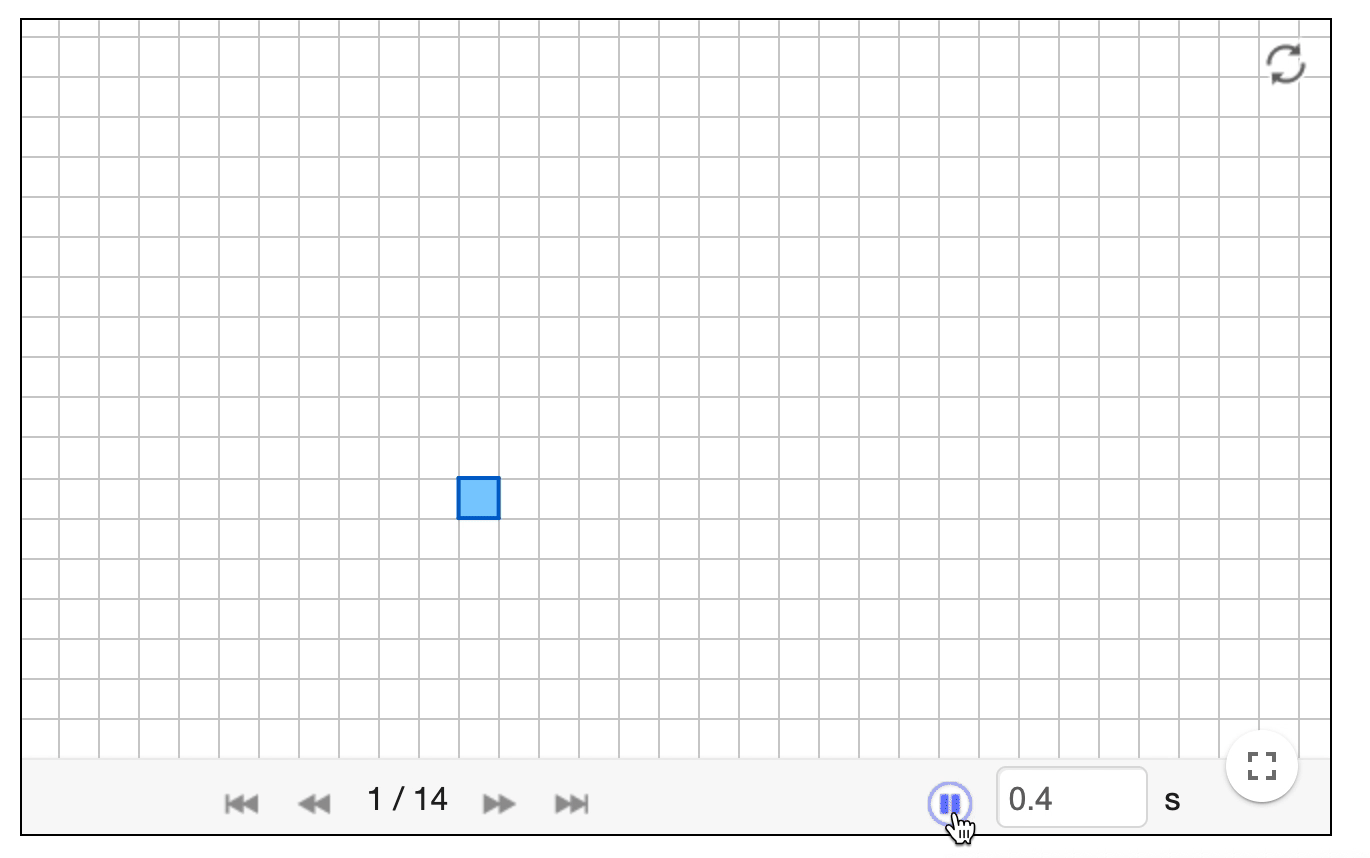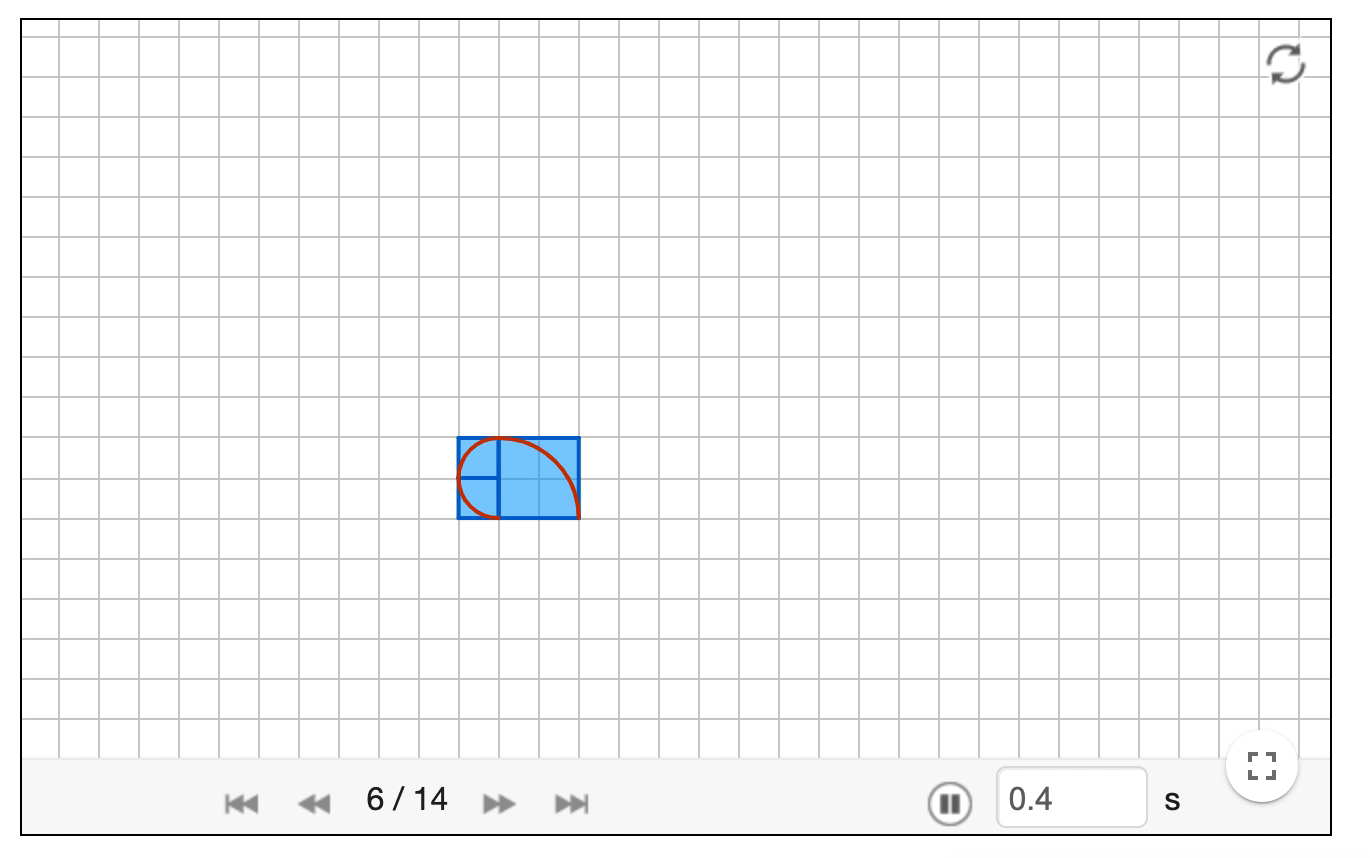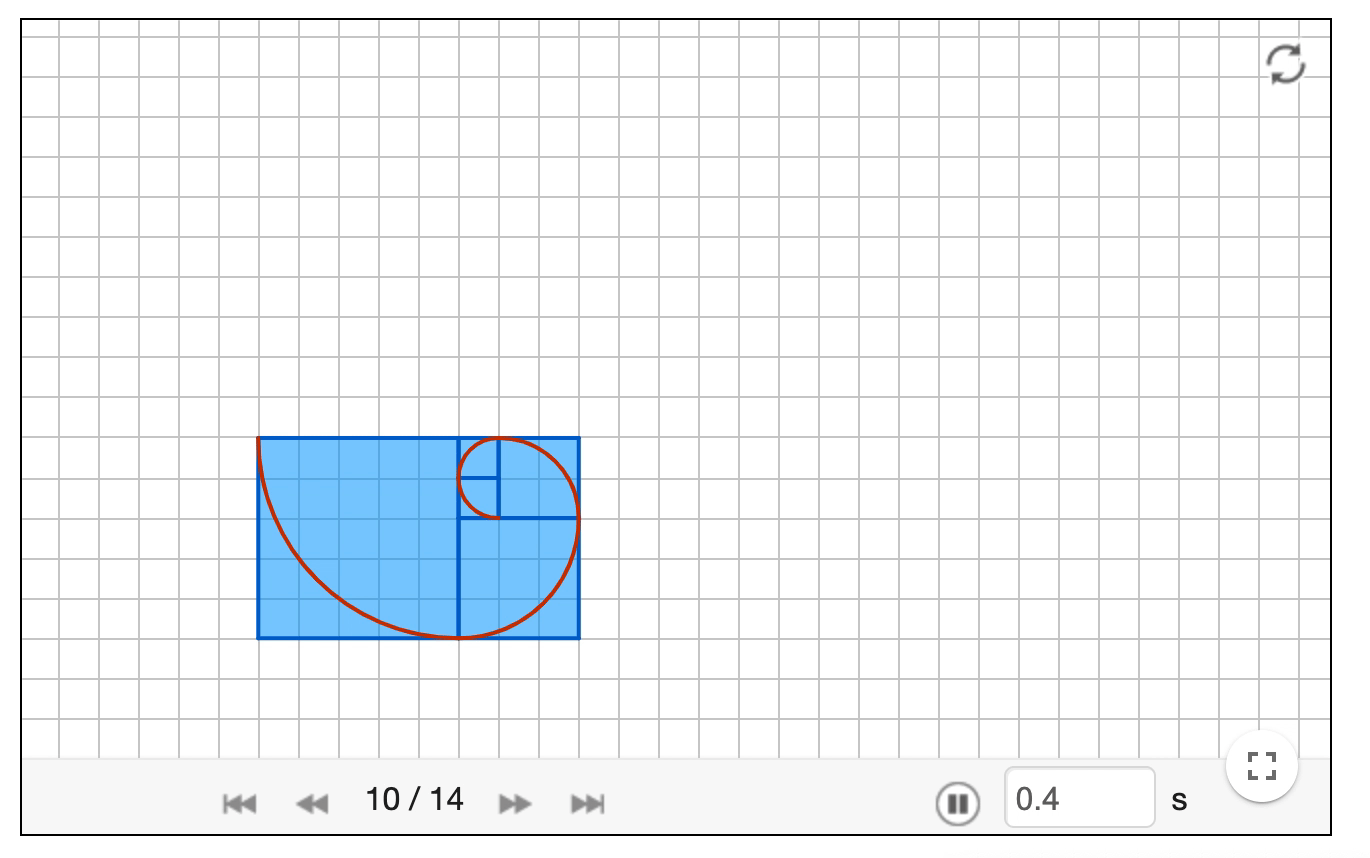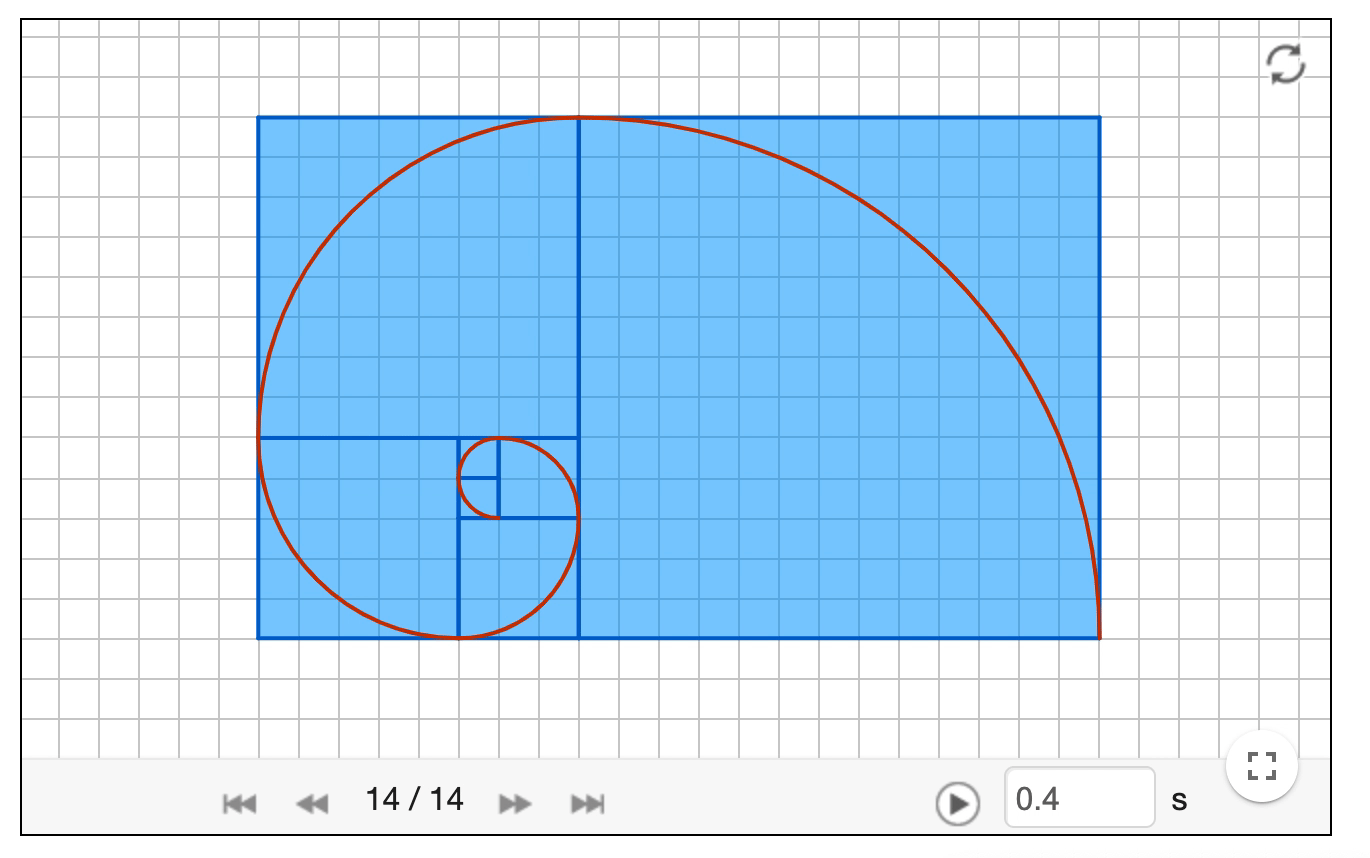
上图只是绘制到了10多项,如果继续绘制,会变成下面这样。。

另外斐波那契数还有一个神奇的性质,f(n-1)/f(n)约等于黄金分割比例,n越大,其越接近黄金分割比0.6180339887…… 。
扯远了,回到今天的正题,如何求斐波那契数列第n项,如果作为面试题的话,也可以考察候选人很多方面,比如递归、优化、数学…… 当然现在大厂面试时很大可能也不会直接出斐波那契了,而是可能出现其变形,文末会给出几个相关参考题。
求解斐波那契数列第n项有很多种方式
递归求解
根据其递归定义,我们很容易写出以下递归函数来计算斐波那契第n项。
private static long fibonacci(int n) {
if (n == 0) {
return 0L;
}
if (n == 1) {
return 1L;
}
return fibonacci(n-1) + fibonacci(n-2);
}虽然按其数学定义来看,代码是没问题,但这种实现效率非常低,存在着大量的重复计算,不信你用你自己电脑执行下fibonacci(30) 试试! 哦,对了,如果面试官让你分析下上述代码的时间复杂度,你会分析吗??
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)像上图中,fib(3) fib(2) 被重复计算多次,实际上对于任意n,其n-2节点都会出现在其左右子树中。大致看起来递归求斐波那契数列的时间复杂度为O(2^n),这个也不是精确上界,精确证明见递归求解斐波那契数列的时间复杂度——几种简洁证明
当然递归版本也有有方法优化的,我们之前打ACM的时候有种方法叫做记忆化搜索,其本质上就是把计算结果缓存下来,下次用的时候就直接取,而不是重复计算,这样可以避免上述代码中大量的重复计算,可以将其时间复杂度从O(2^n) 降至 O(n)。针对上面代码的改动也很简单,你可以自己试试(提示:就是加个全局数组保证下结果)。
递推求解
我们在解决问题的时候,逆向思维也很重要,逆向思维往往能找到更高效直接的解决方案。上述递归的方式其实是从后往前计算,事实上我们可以从前往后计算。居然我们已知f0和f1,那我们就可以算出f2,紧接着算出f3 f4,一直到fn。
private static long fibonacci(int n) {
long[] fb = new long[n+1];
fb[1] = 1;
for (int i = 2; i <= n; i++) {
fb[i] = fb[i-1] + fb[i-2];
}
return fb[n];
}不过上述代码依旧有优化空间。我们计算fb[i]只需要fb[i-1]和fb[i-2]两项即可,是不是0到i-3都白存了!其实只需要保存长度为2的滑动窗口即可,优化后代码如下:
private static long fibonacci(int n) {
if (n < 2) {
return n;
}
long fa = 0L;
long fb = 1L;
long fc = fa + fb;
for (int i = 2; i < n; i++) {
fc = fa + fb;
fa = fb;
fb = fc;
}
return fc;
}比内公式
其实斐波那契第n项是有计算公式的,称为比内公式,如下:
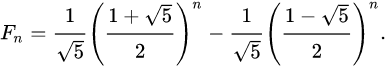
在维基百科Fibonacci number上有严格的证明过程,有兴趣可以参考下。但这个公式其实并不适合计算机来计算。首先,根号5是个无理浮点数,众所周知当今的计算机在处理浮点数时是有精度损失的,另外计算机计算浮点数的速度也比较慢。当然,你也别惦记着把这个公式背下来,你面试过程中不一定能想起来这个,当然如果你是数学大牛的话,你可以参考下推导过程,直接在面试现场把结论推导出来,肯定能唬住大部分面试官的。
矩阵幂运算
上面已经说了比内公式有低效和精度损失的问题,我这里当然有更牛x的方案了,那就是借助矩阵的运算来解决,借助如下公式,我们可以计算出斐波那契的第n项。
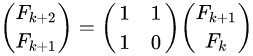
如果再进一步,公式可以化简为:
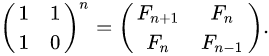
具体推导过程见维基百科Fibonacci number,当然这里我直接用octave验证过了,毫无问题。
>>fb = [1,1;1,0]
fb =
1 1
1 0
>>fb^10
ans =
89 55
55 34
>>fb^30
ans =
1346269 832040
832040 514229小学三年级的时候我们学过求n次方的快速幂算法,可以把求n次方的时间复杂度从O(n)降低到O(log(n)),对于矩阵我们当然也可以用快速幂算法(不知道快速幂的同学可以去复习下了)。
// 快速求矩阵的n次方
private static long[][] pow(long[][] matrix, int n) {
if (n == 1) {
return matrix;
}
long[][] res = pow(matrix, n/2);
res = multi(res, res);
if (n%2 == 1) {
res = multi(res, matrix);
}
return res;
}
// 两个矩阵相乘
private static long[][] multi(long[][] m1, long[][] m2) {
long[][] res = new long[2][2];
res[0][0] = m1[0][0]*m2[0][0] + m1[0][1]*m2[1][0];
res[0][1] = m1[0][0]*m2[0][1] + m1[0][1]*m2[1][1];
res[1][0] = m1[1][0]*m2[0][0] + m1[1][1]*m2[1][0];
res[1][1] = m1[1][0]*m2[0][1] + m1[1][1]*m2[1][1];
return res;
}
public static void main(String[] args) {
long[][] fb = {{1,1},{1,0}};
long[][] res = pow(fb, 10);
System.out.println(res[0][1]);
}上述几种解法把时间复杂度从O(2^n)降低到了O(log(n)),实际上还有O(1)的解法。斐波那契数列其实是一个增长很快的数列,n用不了多大就会超过int甚至long所能表示的范围(n大概几十就会溢出),所以可以直接存下来,用的时候直接取,用空间换时间,从而达到O(1)的时间复杂度。
面试题扩展
求斐波那契第n项虽然看起来很基础,但它也有着很高级的解法,平凡中蕴藏着不凡。事实上,你现在出去面试,大概率不会遇到面试官直接问你斐波那契,而是其变形题或是和其他内容融合的题,比如:
- 你每次可以上1级台阶,或者2级台阶,问:上到第n级台阶总共有多少种不同的路径?
- fib(i)对应的是斐波那契的第i项,找到所有第fin(i)个素数(i<=20),比如fib(20)是6765,第6765个素数是67931。
欢迎关注我的面试专栏面试题精选,永久免费 持续更新,本专栏会收集我遇到的比较经典面试题,除了提供详尽的解法外还会从面试官的角度提供扩展题,希望能帮助大家找到更好的工作。另外,也征集面试题,如果你遇到了不会的题 私信告诉我,有价值的题我会给你出一篇博客。