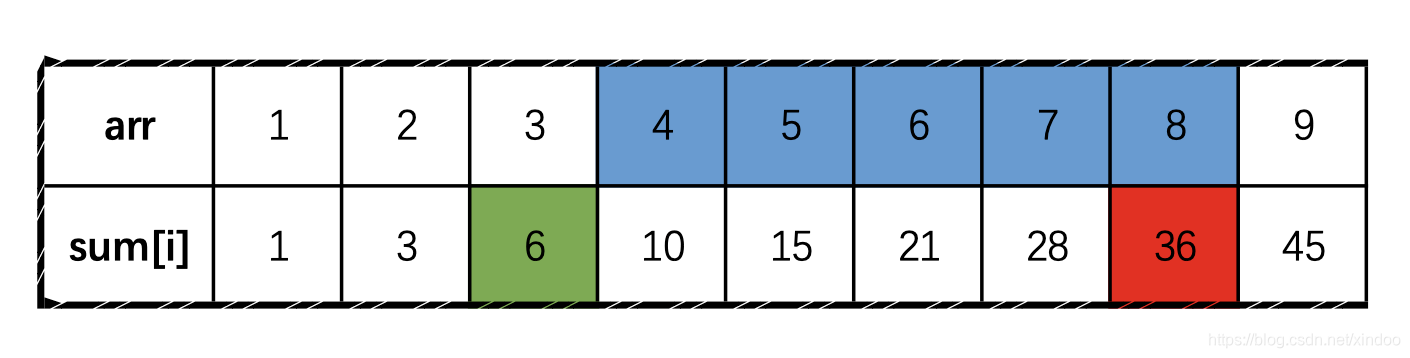
前两天在一个学长面试的时候遇到这样一个题,这里稍微详细说下本文的标题。给你n个任意整数,求排序后相邻两个数之间的最大差值,这里n可能有10^5,整数为任意32位整型。要求求解算法的时间复杂度为O(n)。
O(n)的时间复杂度,再加上任意32位整型,意味着我们没法用桶排序、计数排序等O(n)的排序算法(还记得这些算法吗!),当我看到这题的时候,我优先就排除了排序,也排除的桶排序,从此在错误的道路上越走越远,直到看了别人的题解。我这里再写一题解是因为别人的题解只有解决方法,没有思考过程。
回到题目, 首先说明一点,这题的大体思路就是桶排序,但是,不需要全部排序,只需要大体有序,其实就是每个桶内的数不需要有序,接下来我将解释为什么桶内的数不需要排序。
n个任意的数,划分到n个桶里。首先第一种情况,如果恰好每个桶都只有一个数,划分后不就恰好有序了吗,有序这道题不就好解决了吗! 另一种情况,在每个数数值范围非常大的时候也是很常见的,就是数不会均匀的落到每个桶中,这题的主要难点也在这。
如何解决? 想想看,在任意一个桶内任何情况下任意俩数的最大差值是多少,最大不就是桶的大小减一吗? 但是,在全局中肯定存在两个桶,后面一个桶的最小值和前一个桶的最大值差值大于桶大小,且这两个桶之间不存在其他有数存在的桶。 换种牵线的说法,绝对存在bucket[j].min - bucket[i].max > bucket[i].size-1(j > i且 i和j之间无其他非空桶)。理解了这点,此题得解。
其实我们只需要遍历次数组,找出最大最小值,然后安装最大最小值,将其他数划分到n个桶里。然后求连续两个非空桶i j的bucket[j].min - bucket[i].max的最大值即可。
想想看,因为我们只需要用到每个桶的最大最小值,所以不需要在每个桶中保存所有的值,只需要最大最小值而已。 有了思路,代码编写其实并不复杂,这里我就不写了(其实是懒得写)。。。