前两天在刷leetcode的时候,遇到了一题Implement Rand10() Using Rand7(),rand7()可以给你等概率返回1-7的任意一个数,让你用rand7()实现一个rand10(),rand()可以等概率返回1-10的任意一个数。后来又在上网中不经意看到了另一题rand5()实现rand7(),更早些,我自己面试的过程中也遇到过类似的题。再早些在大二的时候,有个学姐在群里问过的一道她遇见的一道类似的面试题,我们先来从这道题开始,逐步剖析这种randX()-->randY()的题目怎么做。
当年网协有个09级的学姐面试时遇到一个问题,有个unFairRand()函数以80%的概率返回0,20%的概率返回1,请在unFairRand()的基础上实现一个fairRand(),能够以50% 50%的概率返回0和1,不允许使用各其他random函数。当时我给出了一个正确的解答,但没做过详细分析。
我的解答是这样的,用两次调unFairRand结果的组合来返回0或者1,两次结果是01就返回0,10就返回1,00或者11就重新算一次。01和10的概率都是16%。算一次就返回0和1的概率是32%,但还有68%的可能再算一次。不过不用担心,我们构造的函数不管内部计算多少次,只要返回1或者0,其概率是一样的,这也满足题目要求,代码如下。
public int fairRand() {
int x = unFairRand();
int y = unFairRand();
if (x == 1 && y == 0) {
return 1;
}
else if (x == 0 && y == 1) {
return 0;
} else {
return fairRand();
}
}
这时候让你算下,调用一次fairRand()后,unFairRand()被调用的期望是多少?公式如下,这个公式可以化简,貌似是高中的知识了,感觉我是化不出来了。
$$
E = 0.322 + 0.680.324 + 0.680.326 + .... +0.68^{(n-1)}0.32*2n \ \ (n \rightarrow \infty)
$$
接下来我们直接看下leetcode上这道Implement Rand10() Using Rand7(),rand10()除了严格等概率返回1-10之外,起始还限制你尽可能少调用rand7()。
调用两次加在一起,然后模10+1?貌似1-10的数字都有了,来看下分布表。
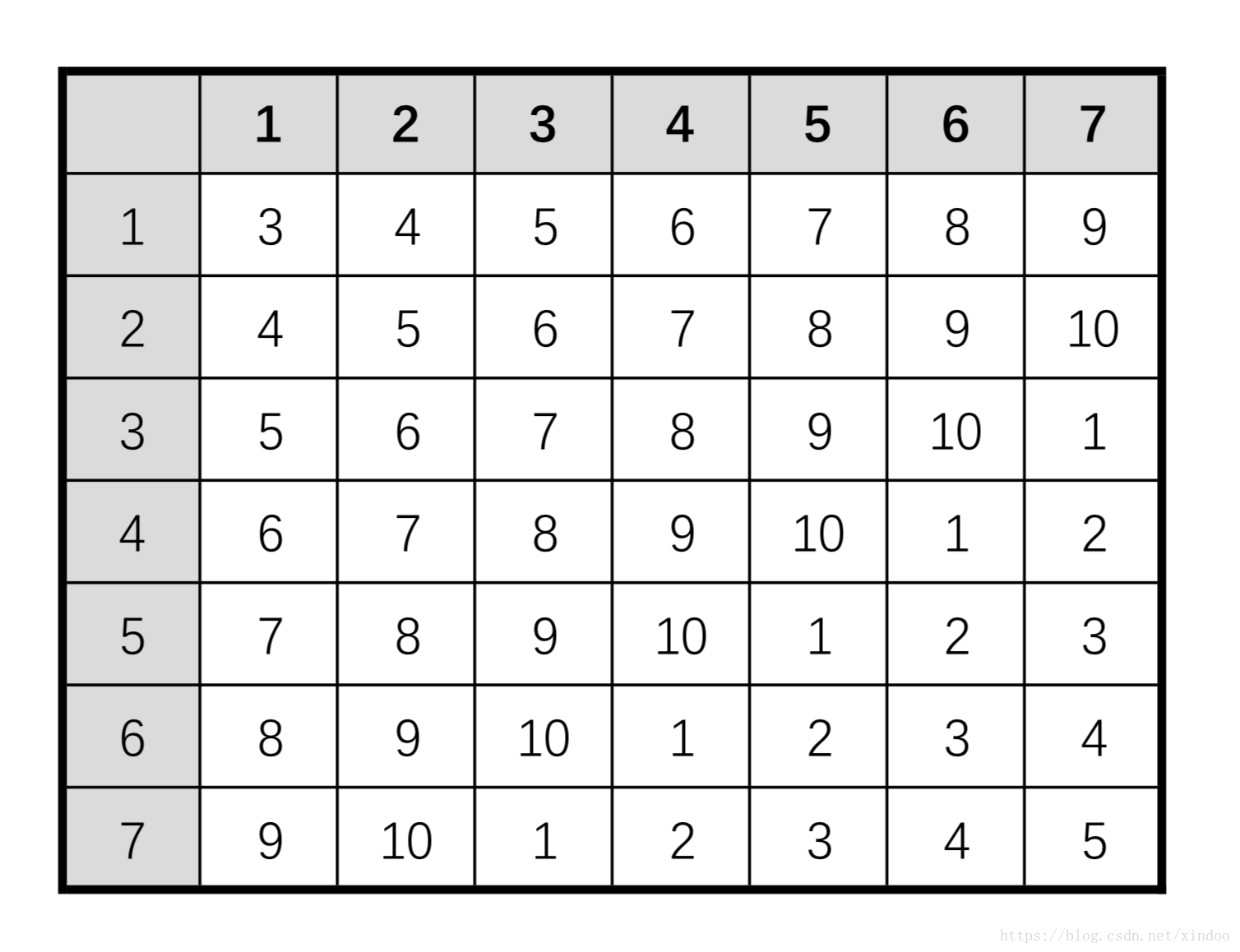
明显可以看出,1-10每个数字分布肯定不是相等的。我们必须构造出一数表,使得1-10任意一个数在表里出现的频率是一样的,如下,构造出一个连续数表就可以了。
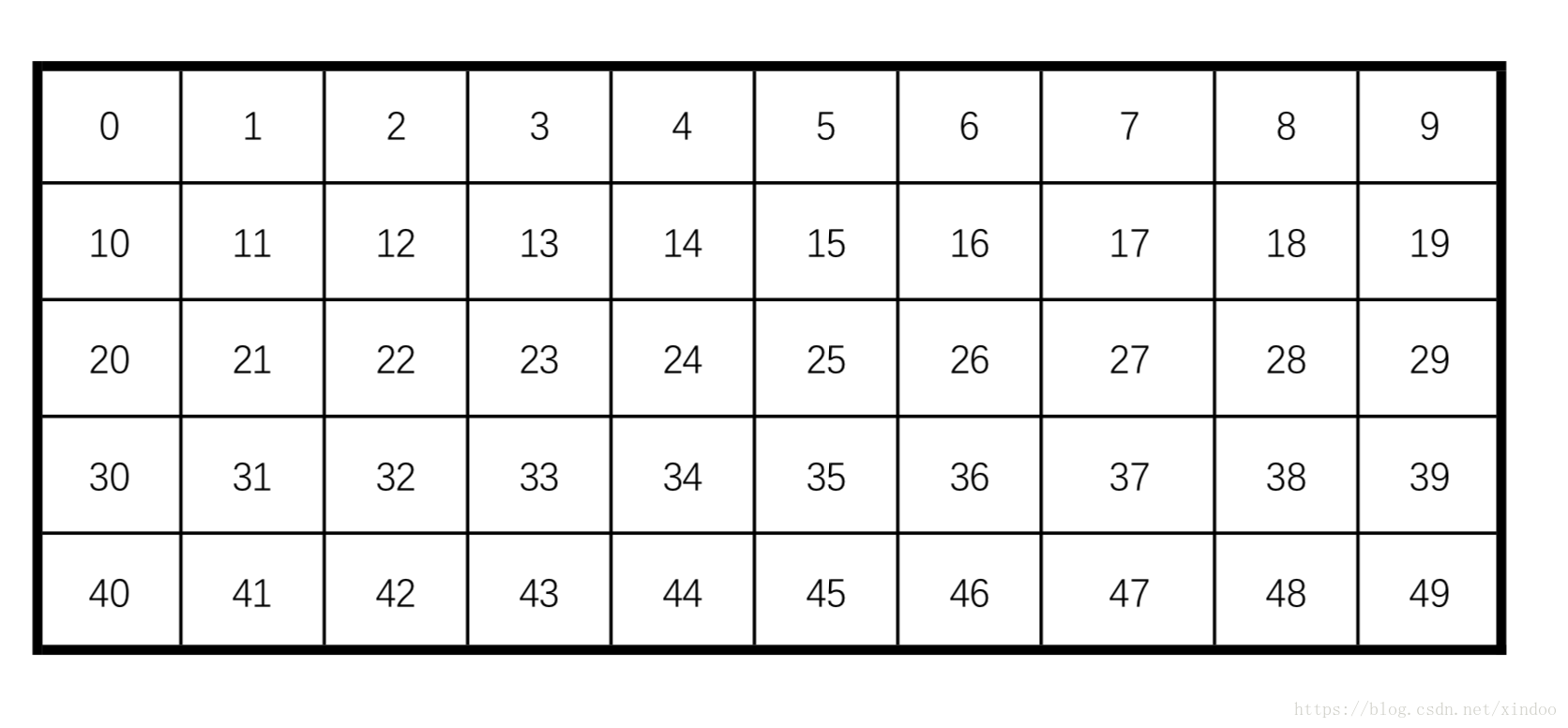
如何构造,(rand7()-1)*7 + rand7(),就可以了,为什么是乘以7而不是6或者8,如果乘以其他的数,数表里的数就会有缺失或则重复计算,概率必然不一样了。举个例子,乘以8,14、15就多出现了。
Implement Rand10() Using Rand7()的解答如下。
public int rand10() {
int x = (rand7()-1)*7 + rand7();
return x<=40 ? x%10 +1 : rand10();
}
如果是rand5-->rand7呢?简单
public int rand7() {
int x = (rand5()-1)*5 + rand5();
return x<=21 ? x%7 + 1 : rand7();
}
为什么上面分别是x<=40和x<=21,而不是其他数字里,起始rand10里10,20,30,40都可以,rand7里7,14,21都可以。回顾下题目还有另一个要求,尽可能少调用给你的rand函数,从概率的角度来看,取的数越大,需要再次计算的几率就越小,调用给定函数的次数就越少。
至于调用次数的期望,我只给出rand7计算rand10的期望表达,rand5->rand7就留给你算了。
$$
E = 2\frac{40}{42} + 4\frac{2}{42}\frac{40}{42} +....+2n(\frac{2}{42})^{n-1}*\frac{40}{42} \ \ \ \ \ (n \rightarrow \infty)
$$
如果是randM --> randN (M < N)呢?也简单。
public int randN() {
int x = (randM()-1)*M + randM();
return x <= N*a ? x%N +1 : randN(); //这里a是使得调用次数最少的一个系数
}