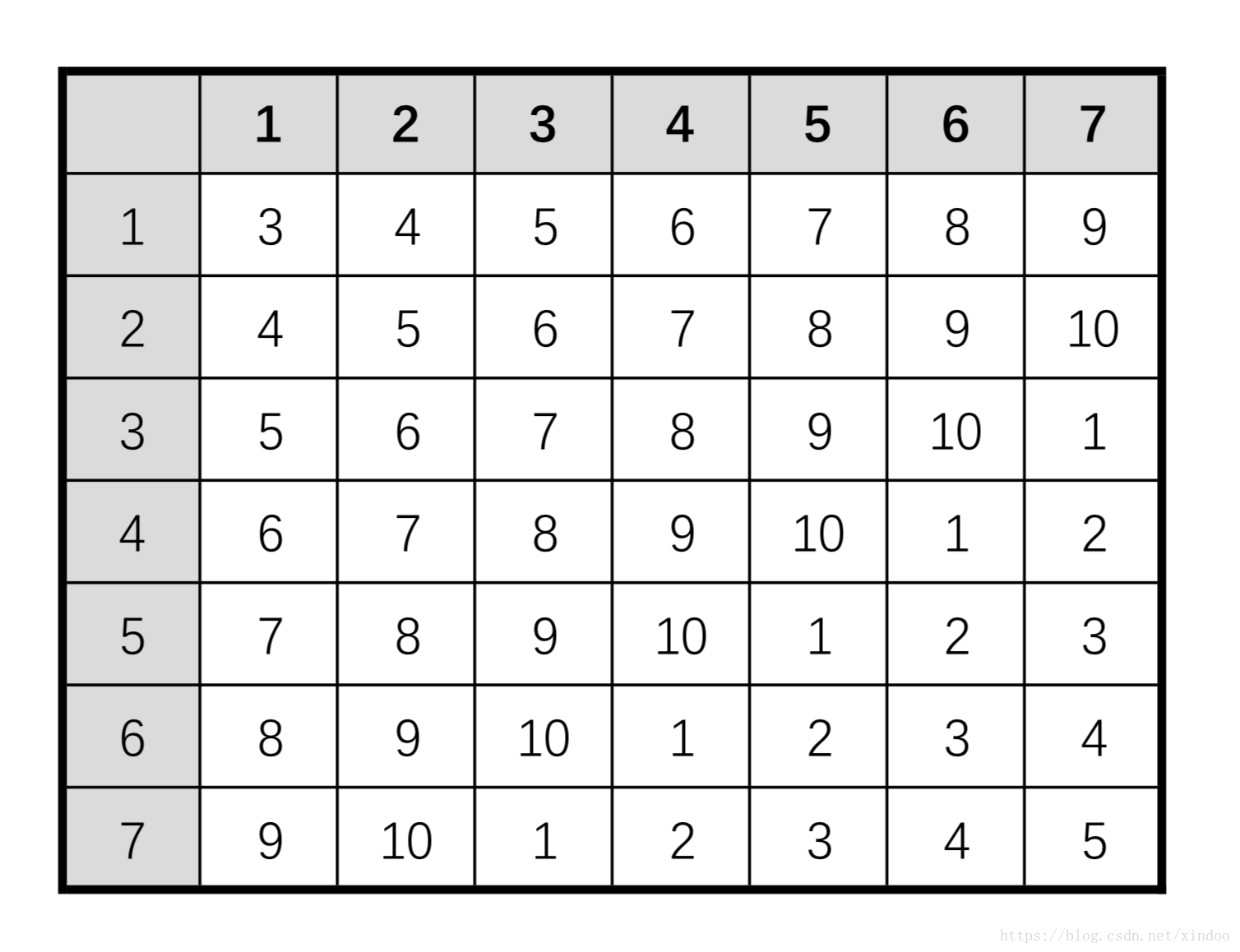
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
Integers in each row are sorted in ascending from left to right.
Integers in each column are sorted in ascending from top to bottom.
此题是74题Search a 2D Matrix的升级版,所给出的矩阵性质相对74题少了一条,只保证了每行和每列都是增序的,但依旧有O(m+n)的解法。
具体思路就是每一行倒着扫,扫到第一个比target小的数就跳到下行,如果等于当然是直接返回true了,如果下一行还比target小就继续跳下一行,直到最后一行。
为啥这么做是可行的? 可能我比较笨,想了半天才想到。 因为每一列都是增序的,举个例子,假设matrix[0][5] > target,那么[0][5]位置右下(包含右和下)所有元素不可能比target小。
直接上代码
public class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int row = matrix.length;
if (0 == row)
return false;
int col = matrix[0].length;
int i = 0;
int j = col-1;
while (i < row && j >= 0) {
while (j >= 0 && matrix[i][j] >= target) {
if (matrix[i][j] == target)
return true;
if (j > 0)
j--;
else
break;
}
if (i < row-1)
i++;
else
break;
}
return false;
}
}